N-queen
- queen 을 겹치지 않게 놓는 문제이다.
- 시간복잡도는, 모든 row 에서 모든 column 에 대해 검사하므로, O(N^N) 이다.
풀이
코드 구조
- queen 을 놓기 전에, 이전 queen 들의 위치와 비교하여 놓아도 되는지 검사한다.
- 되면 queen 을 놓는다 (함수 호출, DFS 탐색)
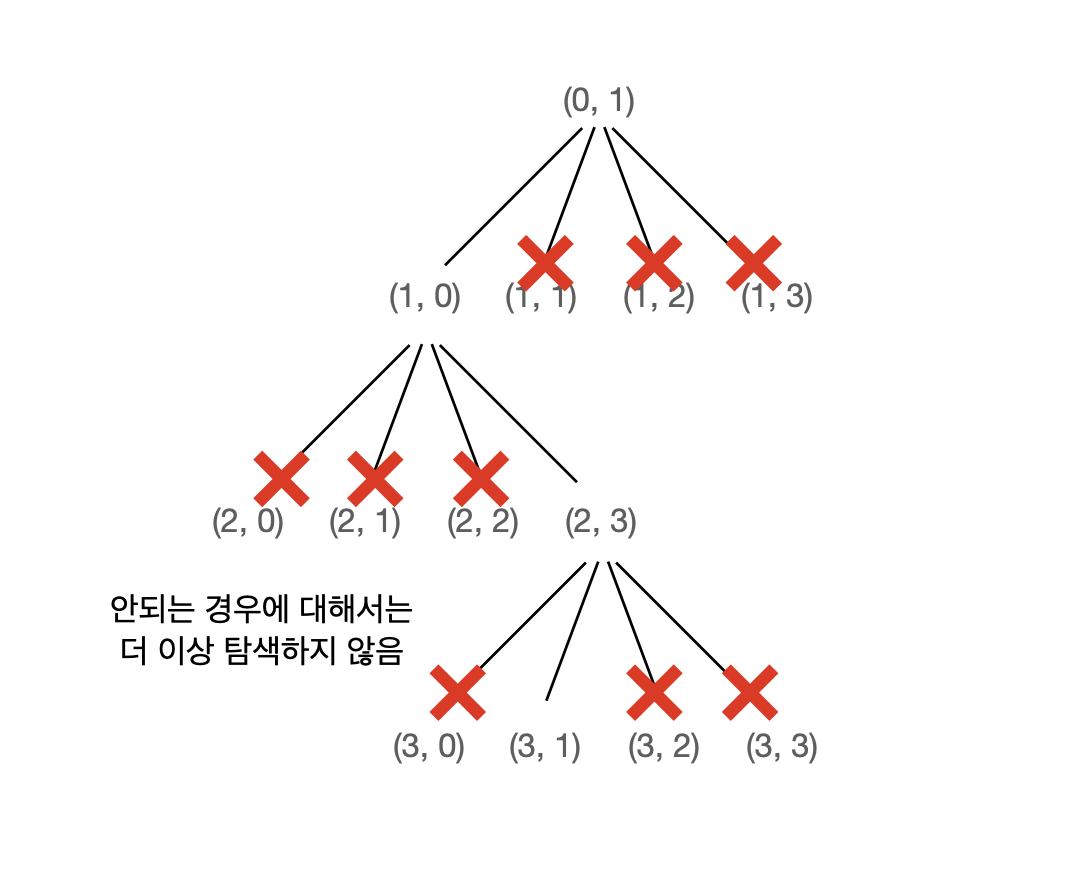
- 안되면 더 이상 함수호출을 하지 않는다 (끝 = 가지치기)
가지치기는 어떻게 되는가
check 함수에서 여기(newRow, newCol) 에 queen 을 놔도 되는지 검사를 한다. 이때 queen 을 놓아도 된다고 판단되면 계속해서 함수 호출을 하고 (DFS 탐색), queen 을 놓으면 안된다고 판단되면 거기서 끝낸다.
따라서 그 상태에서는 더 이상의 함수 호출이 없으므로, 가지치기가 된다.
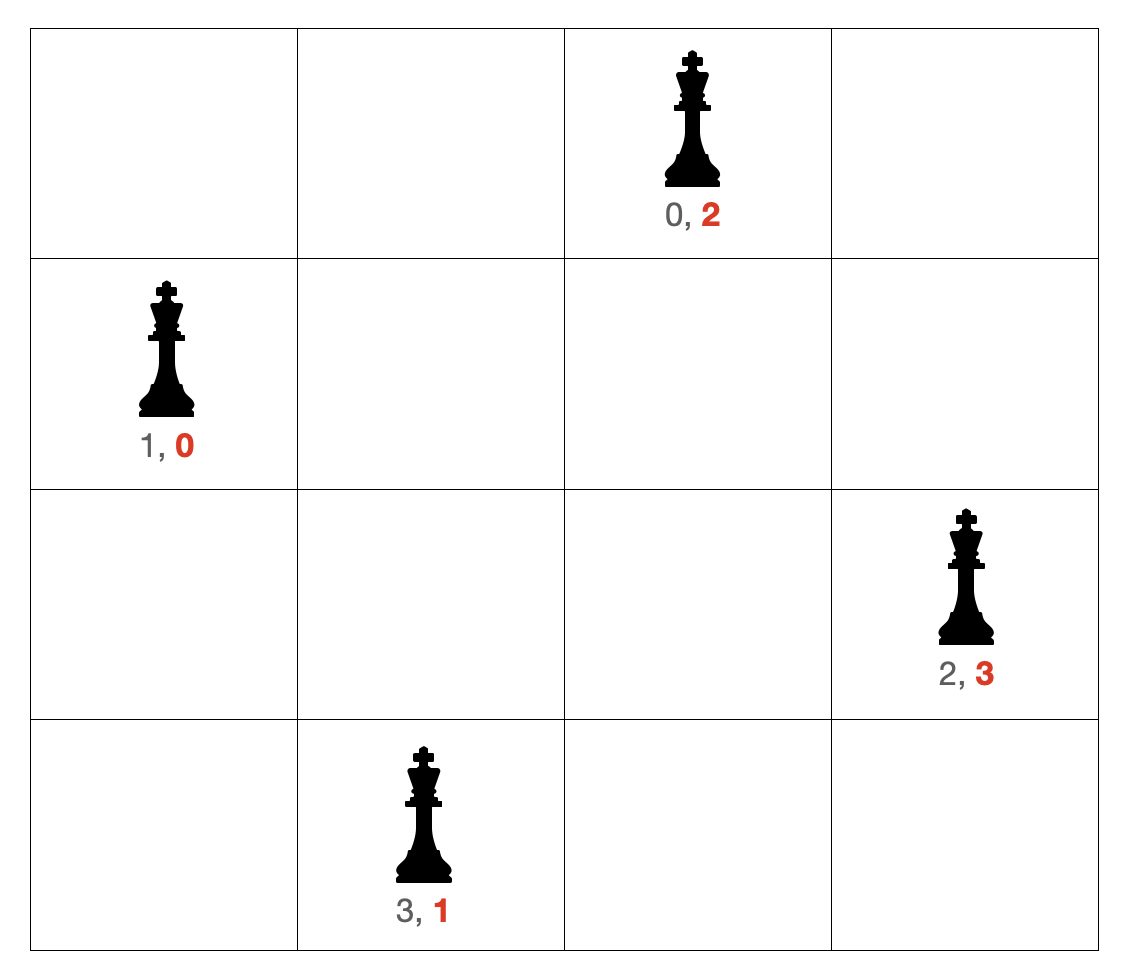
queen 의 위치 관리를 1차원 배열만으로 가능한 이유
queen 은 한 row 에 하나밖에 놓지 못하기 때문에, queen 의 위치는 1차원 배열로 생각할 수 있다. index 를 row 로, queenPos[index] 를 col 으로 생각하는 것이다.
예를들어 queenPos = [2, 0, 3, 1] 라면 queen 은 그림과 같이 (0, 2), (1, 0), (2, 3), (3, 1) 에 있는 것이다.
코드
let ans = 0;
let N = 0;
function solution(n) {
const queenPos = new Array(n);
N = n;
queen(0, queenPos);
return ans;
}
function queen(step, queenPos) {
// step == N 인 이유는, 마지막 step(==N-1) 까지 queen 을 놓고 step(==N) 와서 이 조건문에 걸려야 하기 때문이다.
// 만약 step === N+1 이면 영원히 끝나지 않을 것이고,
// 만약 step === N-1 이면 마지막 row(step) 에 도달하기만 해도 퀸을 놓은 것으로 판단할 것이다.
if(step === N) {
ans++;
return;
}
// 현재 step (row) 에서 놓을 수 있는 queen 이 뭐가있는지 볼건데
for(let col = 0; col< N; col++) {
// 먼저 검사를 하고
if(check(step, col, queenPos)) {
// 놔도 되면 놓고, 그다음에 다음 step(row) 에 queen 을 놓기 위해 함수를 호출한다.
queenPos[step] = col;
queen(step+1, queenPos);
}
// 퀸을 놓으면 안되면... 그냥 끝. (= 가지치기, 현재 상태에서 더 이상의 함수 호출은 없다)
// 아래를 더 볼 필요가 없기 때문이다.
}
}
function check(nextRow, nextCol, queenPos) {
for(let prevRow=0; prevRow<nextRow; prevRow++) {
const prevCol = queenPos[prevRow];
// 대각선 검사
if(Math.abs(nextRow - prevRow) === Math.abs(nextCol - prevCol))
return false;
// column 검사
if(prevCol === nextCol)
return false;
}
return true;
}연습용 체스판 PDF (출력해서 쓰세요)
아래 두 종류를 각각 두 장씩 만들어놨으니 필요한 부분을 양면인쇄 하시면 됩니다.
체스판 출처 https://www.freeprintable.com/print/free-printables/blank-chess-board


'알고리즘 Algorithm' 카테고리의 다른 글
| [프로그래머스] Lv.3 가장 먼 노드 (BFS) + 시간초과, 메모리초과 해결 (0) | 2023.02.25 |
|---|---|
| [프로그래머스] Lv.2 배달 (다익스트라) (0) | 2023.02.18 |
| [프로그래머스] Lv.2 게임 맵 최단거리 (BFS) + 반례 14개, 연습용 좌표판 PDF (2) | 2023.02.03 |
| [프로그래머스] Lv.2 모음사전 (완전탐색) (0) | 2023.01.16 |